Definition
Related Definitions
Time Value of Money (TVM)
What is Time Value of Money?
The time value of money (TVM) could be defined as preference to receive money today rather than receiving the same amount at some point in future.
For example, investors are asked to receive $200 today and $200 at some future date, they will choose to receive the amount today as they can earn interest on the same and grow the amount higher than $200 at a future date.
Why is TVM Important?
TVM makes the centre stage for more advanced financial concepts such as the famous discounted cash flow (DCF) that constitutes the foundation stone for many financial models.
Just like DCF, companies use many other advanced financial concepts such as Net Present Value (NPV), and Internal Rate of Return (IRR) which use TVM as an underlying concept.
TVM Calculations
As time value of money normally relates to the value of money across different time horizons, it uses some basic inputs such as the rate of interest per period, number of periods, the present value, and the future value of the money.
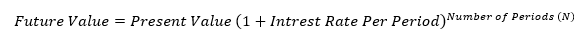
For example, let us assume that we have $100 to invest for one-year on a bank deposit that is currently offering 5 per cent interest per annum (p.a.). How much money would we have at the end of the year?

i.e., $105.
Furthermore, it is also possible to rearrange the above formula to derive at the present value of a future value.

For example, let us assume that we want our bank account to have $500 at the end of a period, and we want to know how much we should save at the beginning of the year to have that amount. Also, let us assume that at present we can earn about 5 per cent on our savings.
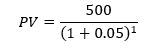
i.e., $476.19
Effect on Compounding On TVM Calculations
Compounding could be simply defined as interest on interest and is a concept which can drastically change the result of either the present value or the future value.
Simply stated, it is not necessary that an investor would receive only annual interest on invested money. Also, it is also not necessary that an investor would invest only for one year. Therefore, interest received on the saved money could change, and so is the period of investment.
Now, an investment could pay interest for more than once in a year. For example, a debt instrument could pay monthly interest, which leads to a compounding of 12 times a year.
Thus, TVM calculations tend to result in a different value for the same amount of investment depending upon the Frequency of Compounding
Many banking or financial institutions denote the interest rate in annual terms which is generally known as the stated annual rate or the quoted interest rate.
Therefore, the state annual rate generally requires conversion into a monthly interest rate for TVM calculations. While monthly is just an example, an investment may pay interest semi-annually, quarterly, even daily.
Hence, the Interest Rate per Period could be derived by dividing the stated annual rate by the number of times interest payment is expected.
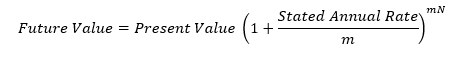
Therefore, to account for the change in the frequency of compounding and the associated number of periods, financial analysts typically use the above notion for TVM calculations.
Where m = number to times interest payment is expected.
So, for example, if a bank deposit offers a stated annual rate of 8 per cent compounded quarterly, and we deposit $10,000 for two years. The FV of our investment in two years will be
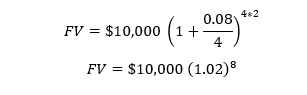
i.e., $11,716.59
The Cash Flow Additivity Principle
The cash flow additivity principle states that amounts of money indexed at the same point in time are additive. The same principle is one of the most important concepts in the time value of money.
To better understand the concept, let us try to calculate the future value of 3 cash flows at T =3.
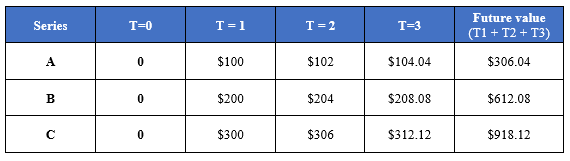
Let’s assume three investors A, B, and C deposit $100, $200, and $300, with the current rate of interest on their investment is 2 per cent.
At T=3, investor A’s total amount would become
$306.04 [100*(1.02)2 + 100*(1.02) + 100]
Likewise, Investor B’s total amount at T=3 would become
$612.08 [200*(1.02)2 + 200*(1.02) + 200]
To calculate the return of the investor C at T=3, the future value of the present $300 investment would be
$918.12 [300*(1.02)2 + 300*(1.02) + 300]
Or else, as the amounts of money are indexed at the same point, we can simply add the future value of investor A’s and B’s to reach the same result as when calculated using the Additivity principle.
$306.04 + $612.08 = $918.12
However, while using the cash additivity principle, one has to make sure that the initial investment amount must be equal to the sum of other initial investment.
