Definition
Related Definitions
Sortino Ratio
What is The Sortino Ratio?
Named after Frank A. Sortino, the Sortino ratio is defined as a variant of Sharpe ratio that segregates the volatility of a portfolio on the negative side from the overall volatility. It does so by using an asset’s standard deviation on the downside or by using the negative standard deviation.
Ideally, just like Sharpe ratio, Sortino ratio could be defined as a statistical tool that is used to evaluate the risk-adjusted return of a portfolio.
Significance of Sortino Ratio
In general, while the overall volatility of a portfolio affects the risk profile of the underlying asset, investors are generally more concerned about the downside risk rather than the overall risk as volatility on the above side relates to a higher return.
Statistically, any fluctuation from the mean return value of a portfolio should be considered as a risk; however, it is the negative volatility which impacts the overall value of a portfolio.
Thus, investors, by nature, are more concerned towards the downside risk, which leads to some statistical concepts like semi-variance, semi-standard deviation, and Sortino ratio.
Calculating the Sortino Ratio
For calculation, the Sortino ratio is calculated by considering the difference between the portfolio returns and the risk-free rate and then divide the numerator by the semi-deviation.

Sortino ratio could be used in both the forward-looking sense and as a measure of historical risk. Investors could use the ratio in the forward-looking context by considering the expected return of the portfolio in the equation.
Likewise, investors can use the ratio to study the historical risk of a portfolio by considring the actual return of the portfolio into the equation.
Assume a portfolio with following annual returns.
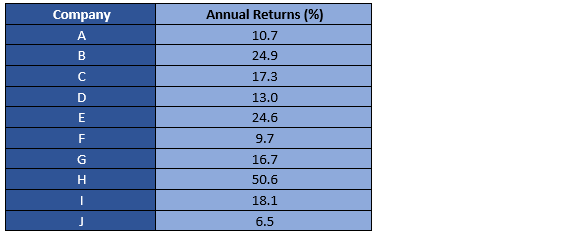
Step 1
The first step involves the calculation of the mean return of the portfolio.
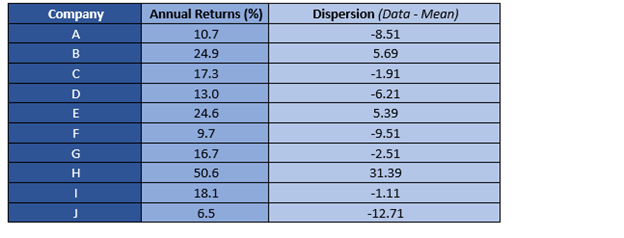
Step 2
Calculate the dispersion around the mean or the excess return above the mean.
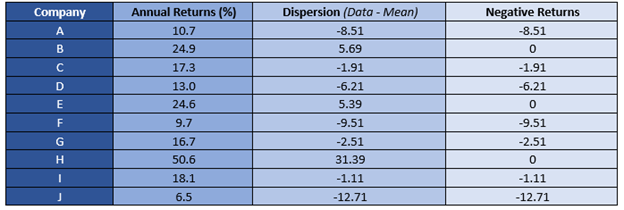
Step 3
The next step post calculating the mean to separate the negative returns from positive returns. The same could be done either manually or by using the IF function in the Microsoft excel as IF(Cell Identifier<0, Cell Identifier, 0).
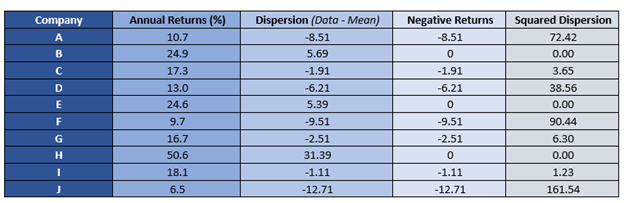
Step 4
Measure the squared deviation of the negative returns.
Step 5
Once we have the squared dispersion of negative returns; the next step is to add them and divide the same by the total number of observations to reach the semi-variance.
So, the squared deviation of negative returns for the series is 374.15.
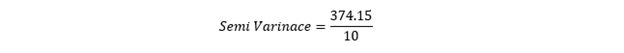
I.e., 37.41
Post calculating the semi-variance; the next step is to calculate the semi-deviation or the semi-standard deviation by taking the square root of semi-variance.
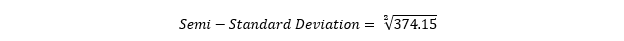
I.e., 6.12
Next, we need the expected return of the portfolio and the risk-free rate. For simplicity, let us assume that the mean return of the portfolio is the expected return or the actual return, and assume the risk-free rate to be 5 per cent.
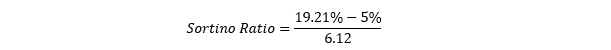
Thus, the Sortino ratio for the above portfolio would be 2.32
On a standalone basis, the portfolio expected return is 19.21 per cent with a 6.12 per cent downside risk. Thus, a ratio of 2.32 means that each unit of risk is covering more than two units of return.
However, as the Sortino ratio is a ratio, it usually makes more sense in the cross-sectional setting, and just like Sharpe ratio, various portfolios in the market could be compared on the basis of their Sortino ratio.
As a thumb rule, a higher Sortino ratio is usually desired as that reflects more units of reward for every additional unit of risk.
Difference Between Sortino and Sharpe Ratio
The Sortino ratio is a variant of the Sharpe ratio as it also utilises the volatility or the risk of a portfolio to measure the performance.
The only difference between both the ratios is that Sortino ratio only focuses on negative dispersion as investors are more concerned about the downside than the upside as compared to the Sharpe ratio that utilises the overall risk to measure the performance of a portfolio.
When Should You Choose Sharpe Over Sortino?
Ideally, in statistics, any deviation from the mean value, be it on the negative side or on the positive side is considered as a risk.
Many institutions tend to give preference to Sharpe ratio over Sortino ratio as it captures the overall risk of a portfolio; thus, tends to give a near to perfect idea of the expected fluctuation in the portfolio return in a forward-looking context.
Likewise, as many investors are usually concerned about the overall value of a portfolio, they tend to focus more on the downside risk as the same decreases the value of a portfolio.
Thus, the use or trade-off between the Sharpe ratio and the Sortino ratio depends upon the risk profile of an investor.
