Definition
Related Definitions
Internal rate of return (IRR)
Internal rate of return (or IRR) is defined as the discount rate that makes the present value of the future after-tax cash flows equal to investment outlay, made initially, by assuming that profit generated from an investment could be reinvested at the same discount rate.
IRR is one of the most frequently used concepts in capital budgeting and security analysis and could also be defined as the discount rate that equates the present value of an investment’s cash inflows with the present value of investment’s outflows.
In simple terms, IRR could also be defined as the discount rate, which makes the Net Present Value (or NPV) of an investment zero.
Apart from capital budgeting, IRR serves as a standard measure of performance in the private equity and private real estate markets in which regular valuations of assets, i.e., daily market prices, are not available.
IRR accounts for both the timing and magnitude of cash flows into and out of an investment or a project.
Calculating IRR
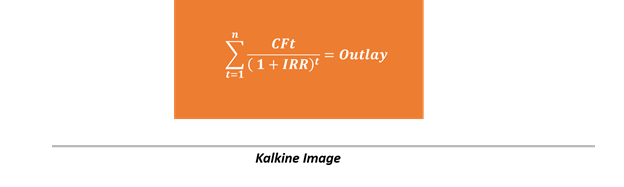
In the above equation, the internal rate of return or the discount rate, equates the present value of the future cash inflows to the initial investment.
The same equation could be rearranged as below:
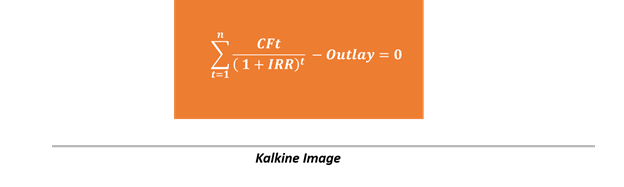
The second equation of the IRR calculation points toward the other definition of IRR, i.e., a discount rate which makes the NPV of an investment zero.
Suppose a Company is considering an investment of $50 million in a capital project that will return after-tax cash flow of $16 million a year for the next four years along with an additional $20 million during Year 5.
The IRR calculation for the above example is as below:
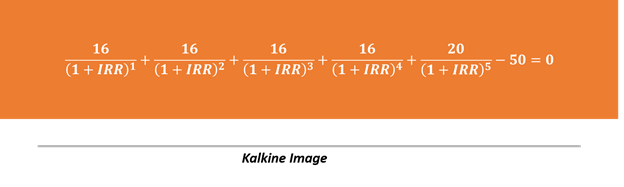
Algebraically solving the above equation could become a troublesome task and could be solved by using a trail and error method, i.e., substituting the value of IRR till the above equation becomes zero.
However, financial analysts generally use various financial calculators such as TA II Plus Professional, Hewlett Packard 12C for calculating the same.
Some analysts also use the IRR feature present in various spreadsheets such as Microsoft Excel.
NPV Profile to calculate the IRR
Suppose a company invests $2.2 million in a project, with an expected cash flow as below
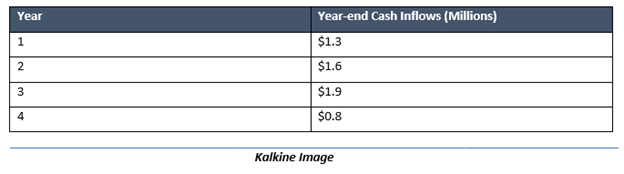
To calculate the IRR of the above problem, we could either utilise the above formula and go for the trail and error method, that would equate the present value of the year-end cash inflows in the above example to the initial outlay of $2.2 million.
Or else, we can build an NPV profile for finding out the same by using Microsoft Excel as below:
For building a NPV profile, the first thing we need is a discount rate or the expected rate of return of an investors. For calculation purpose, assume that the current required rate of return is 8 per cent.
The NPV profile for the above problem is as below
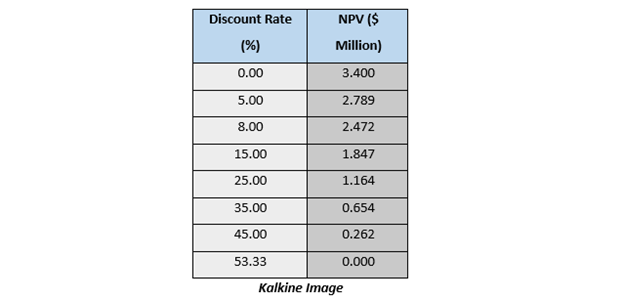
When mapped on a graph, the NPV profile crosses the horizontal line as the discount rate equals the IRR. Thus, the point where the NPV profile crosses the horizontal line is considered as the IRR.
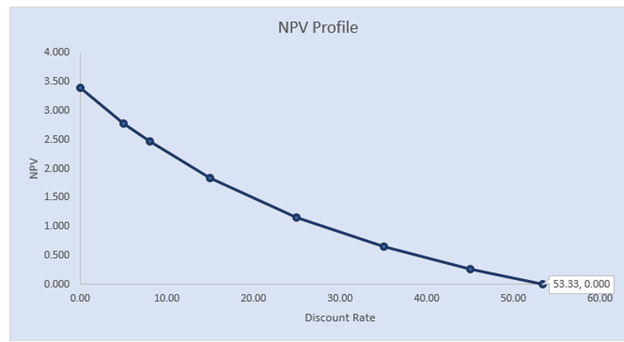
While constructing the NPV profile in Microsoft Excel, one can use various discount rates to reach a zero NPV, use the IRR function to determine the internal rate of return of a series of cash inflows, and can use Goal Seek tool under the what if analysis in the Data tab.

Types of IRR
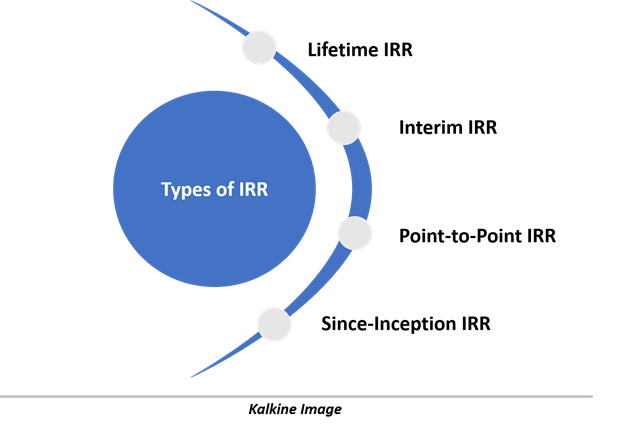
- Lifetime IRR
Lifetime IRR is defined as the IRR of all the cash flows that are available from start to finish of the investment. In this type of IRR, there is no terminal appraised value or residual value. Sometimes the lifetime IRR is also called as the “overall” IRR.
- Interim IRR
Interim IRR is defied as the IRR that assumes an appraised terminal value, i.e., in an interim IRR, period T occurs prior to the end of the investment and an appraised value is used for the period T cash flow.
- Point-to-Point IRR
PTP IRR is defined as the IRR of the time 0 and time T cash flows that are appraised values or are other cash flows during the investment’s lifetime.
- Since-Inception IRR
Since-inception IRR is defined as the IRR calculated since the date of its formation. Since-inception IRR is used for analysing the performance of a fund rather than a project. The cash flow used for the calculation in each period is the aggregate cash flow of all portfolio holdings of the fund.
Investment Decision with IRR
The investment criteria with the IRR is relatively simple, i.e., invest if the internal rate of return is higher than the required rate of return.
Likewise, do not investment if the internal rate of return is less than the required rate of return.
Problem With IRR
- The Multiple IRR and No IRR
In a project or investment with nonconventional cash flow, the IRR could either show multiple values or no value at all, making it difficult to use for a project or investment which frequently changes the direction of cash flows, i.e., changes from cash inflow to cash outflow in middle of the project to investment tenure.
- Scalability issues
The IRR can vary drastically with the scale of cash flows for two different projects that might have a similar cash flow pattern in percentage terms, making it less useful for comparing projects with different magnitude or scale of cash flows.
- Reinvestment Assumption Problem
IRR plainly assumes that the cash flow generated after the initial outlay could be reinvested at the similar discount rate over and over again till the end of the project’s life or investment tenure. However, in reality, that is seldom the case and with the low interest rate environment, every investment faces the reinvestment risk.
