Definition
Related Definitions
Hypothesis testing
What is hypothesis testing?
Hypothesis testing is a process in which an analyst makes inferences or calculated guesses about a specific parameter. Based on the nature of the data and reason for analysis, the analyst decides on the methodology that he/she would follow next.
The primary objective of hypothesis testing is to assess the feasibility of the hypothesis with the help of sample data. The sample data is taken from population data or data generating process.

Source: © Rummess | Megapixl.com
Simplifying hypothesis testing
When we conduct quantitative research, the objective is to answer the research question or test a set hypothesis.
In the process, the analyst tests the statistical sample to prove the feasibility of the null hypothesis. For this, the user tests the hypothesis by measuring and studying sample data out of the population data. The sample data is taken randomly from the population data to test the null and alternative hypothesis.
Terminologies to understand and remember in hypothesis testing
The application of hypothesis testing is there in various fields and situations. However, the situation in each case differs from one another. However, the common thing in each case is the terminology used during the process. Let us look at these common terminologies.
- Null Hypothesis
- Alternative Hypothesis
- Significance
- Power
- Test Statistic
- One-tailed and two-tailed tests
- Critical values
- P values
- Decision
Null Hypothesis
Null hypothesis refers to the statement that explains the probability model generating the data. In this process, we test the possibility of the statement being true to decide whether to accept or reject the alternative hypothesis.
The null hypothesis is denoted by H0. It includes signs like =, ≤, or ≥
Alternate Hypothesis
The alternate hypothesis contradicts the null hypothesis. It depends on the likelihood of null hypothesis testing whether to accept or reject the alternate hypothesis.
It is denoted by the symbol Ha. It includes sign like ≠, >, or <.
Significance level
Significance level refers to the statistical strength of the hypothesis testing. It is also known as alpha, and it defines the possibility that the null hypothesis is denied.
It is characterised as the possibility of incorrect assuming that H0 is untrue.
Test Statistic
Test statistics refers to a random variable calculated from sample data. It is used in hypothesis testing to verify whether to accept or refuse H0.
Test statistics measure the degree of agreement between a sample of data and H0.
One-tailed and two-tailed tests
One-tailed test:
It is a statistical test where the critical area of the distribution is one-sided. The one-tailed test shows that the sample mean would be greater than or less than the population mean. While using a one-tailed test, the analyst tests the probability of the link in one direction of interest and ignores the link in another direction.
The analyst doing one tail test must set H0, Ha and p-value.
Left tailed:
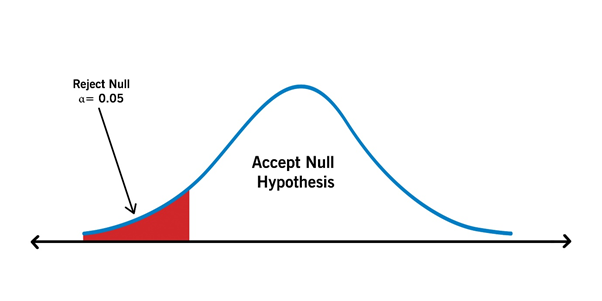
Copyright © 2021 Kalkine Media Pty Ltd.
Right tailed:
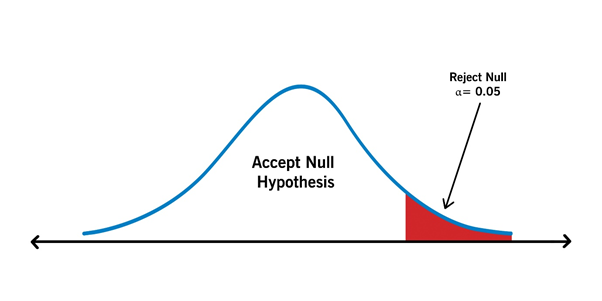
Copyright © 2021 Kalkine Media Pty Ltd.
Two-tailed test:
In a two-tailed test the critical area of the distribution is two-sided. It tests whether the sample is less than or greater than the range of values. While using this in null-hypothesis testing and testing for statistical significance, if the sample tested falls in the range of either of the critical regions, then we choose an alternate hypothesis instead of a null hypothesis.
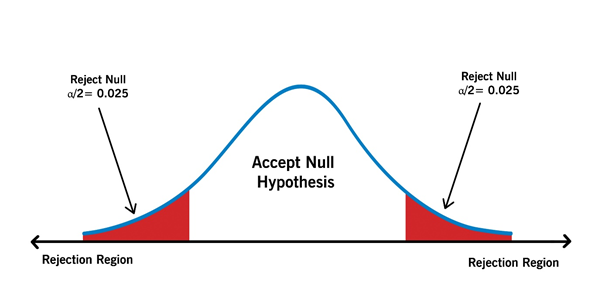
Copyright © 2021 Kalkine Media Pty Ltd.
Critical values
Critical value refers to a position on the test distribution compared to the test statistics to verify if there is a need to refuse the H0. In case the absolute value of the test statistic is more than the critical value, one can deny H0. The critical value corresponds to α.
P-value
P-value helps to support or reject the null hypothesis. The p-value is an indication against the null hypothesis. The smaller the p-value, the stronger the proof to reject the null hypothesis.
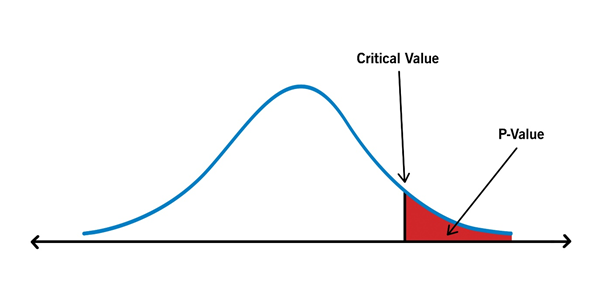
Copyright © 2021 Kalkine Media Pty Ltd.
What are the steps involved in hypothesis testing?
Once the analyst is familiar with the above terms, he/she is ready to test the theory. In this section, we would see the steps to follow while doing hypothesis testing.
Step 1>
The first step involves stating the null hypothesis.
Step 2>
Once we set the null hypothesis, we would then set an alternate hypothesis. Through this step, we would ensure that if the null hypothesis gets rejected, we will choose the alternate hypothesis.
Step 3>
The third step in the process is determining the significance level, which is α. Generally, a significance level of 5% (0.05) is set. However, as per case to case basis, the value may defer. It could also be 0.1 or 0.01.
Step 4>
In this step, we calculate the p-value or the calculated probability of achieving the null hypothesis.
Step 5>
In the fifth step, we draw a conclusion based on the value of p. In case the p-value meets the significance level requirement, then we have to refuse H0 and accept Ha. For example: If the p-value is 0.025 and the significance level is 0.05, then we reject the null hypothesis as the p-value is less than 0.05.
Types of errors encountered during hypothesis testing
In hypothesis testing, there are primarily two types of error- Type I and Type II.
Type I Error:
In Type I Error, the null hypothesis is correct. However, it is rejected incorrectly.
Type II Error:
In Type II Error, the null hypothesis is incorrect. However, it is not rejected.

Copyright © 2021 Kalkine Media Pty Ltd.
