Definition
Related Definitions
Game Theory
What is Game Theory?
Game theory is a mathematical statistical analysis of how individuals react to different circumstances presented to them. Each situation comes with a set of payoffs and the individuals must decide which move to play based on these expected playoffs.
Since these payoffs are known to the players depending on different moves by all the participants, the entire course of action depends on the strategy chosen by the players. This strategy might be incentivising for one and harmful for the other or can be beneficial to both. Thus, the players must decide whether to collaborate, or to work for their own profits.
The concept of game theory has various applications in real life. A game theory set up can help alter an individual’s strategy based on his assumptions about the opponent’s move. Thus, it helps determine a sustainable outcome in a situation where two individuals find themselves at conflict. However, not all game theory set ups can be solved productively as they involve trade-offs between what the players desire.
What are the different terms used in game theory analysis?
- PLAYERS: There are two players in most game theory experiments, and each player is affected by the strategy played by both the players.
- PAYOFFS: Payoffs refer to the outcomes for each player of the game based on different strategies. A payoff matrix depicts the different situations and the associated outcomes by both the players in a diagram form.
- STRATEGY: It refers to the course of action adopted by the players depending on the payoff matrix known by them. It can be for personal profit or in collaboration with each other.
- INFORMATION SET: The players are aware about the possible strategies and the payoffs attached to them. This information forms the information set which is used by the players to choose their moves.
What is Nash Equilibrium?
Nash equilibrium refers to that outcome in the game in which both players have achieved the best possible solution through a collaboration. This is the state from which neither of the players would want to deviate.
This outcome may not always be optimal for both. In certain instances, it might be possible to make one player better off by making the other worse off.
What is Pareto Optimality?
Pareto Optimality refers to that stage in which both players have reached their best potential. This state considers the individual’s best outcome rather than the collaborative best outcome. Thus, it is that state from which it is not possible to make one player better off without making the other worse off. The outcome for both the players is at its best.
A Nash equilibrium may not always be pareto optimal. This means that the outcome which is the collaborative best between both players may not be pareto optimal. Thus, it is possible to deflect from that outcome and make both players reach their personal best.
What are the different types of strategies used by the players?
The strategies in the game can be of two types:
- Pure Strategy: This is the strategy which is fully defined for a player and can be thought of as ‘occurring with full probability’.
- Mixed Strategy: This involves assigning probabilities to pure strategies. This allows players to randomly choose a pure strategy. Thus, pure strategy can be termed as a mixed strategy occurring with probability equal to 1.
How is the concept of game theory applied?
- Prisoner’s Dilemma: The most common application of Game Theory can be seen in the example of Prisoner’s Dilemma. This game involves two prisoners who are not aware about each other’s decisions in the game. Both have been suspected of committing a crime and are held for questioning. The prisoners face different years of jail sentence based on the strategy they choose.
The payoff matrix is as follows:

Here the Nash Equilibrium is achieved when both A and B confess. Thus, (5,5) is the collaborative best that both the players can perform. However, this is not the pareto optimal solution.
The pareto optimal outcome is (1,1) as both players want to serve as less jail time as possible. Thus, it is not possible for one to be better off without making the other worse off if neither one of them confesses.
- Battle of the Sexes: Battle of the sexes is a game where a girl and a boy want to go on an outing together, however the girl prefers going to see an opera while the boy prefers going to a football match. However, going to these places separately does not earn them any payoffs, while going together gives higher payoff to only one of them and not both.
The payoff matrix is as follows:
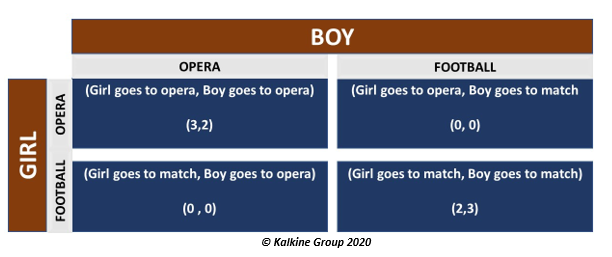
There are two possible Nash equilibria in this game. One is achieved when both go to Opera and the other when they both go to watch the Football match.
Is the concept of game theory accurate?
The limitation of game theory is that it is based on certain assumptions. It assumes that the players would always act in favour of their personal interests. However, it is possible to witness real life scenarios where people are more collaborative as well as altruistic.
It is also possible that in a real life set up, stability is achieved at an outcome which is not a Nash Equilibrium. Depending on the varied social set ups as well as personal preferences, game theory may not always justify real life situation.
